Constraining Power of Cosmological Observables: Blind Redshift Spots and Optimal Ranges
Published in Physical Review D, 2018
Abstract
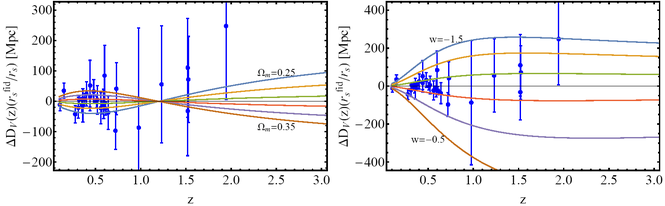
including the effective survey volume , as a measure of the constraining power of a given observable O with respect to a cosmological parameter P as a function of redshift z. We find blind redshift spots zb (
) and optimal redshift spots zs (
) for the above observables with respect to the parameters Ωm, w and gα. For example for
and
we find blind spots at
, respectively, and optimal (sweet) spots at
. Thus probing higher redshifts may in some cases be less effective than probing lower redshifts with higher accuracy. These results may be helpful in the proper design of upcoming missions aimed at measuring cosmological obsrevables in specific redshift ranges.
Cite
If you use any of the above codes or the figures in a published work please cite the following paper:
Constraining power of cosmological observables: blind redshift spots and optimal ranges.
Lavrentios Kazantzidis, Leandros Perivolaropoulos and Foteini Skara
Phys. Rev. D 99 (2019), 063537, arxiv:1812.05356
Any further questions/comments are welcome.
Authors Lists
Lavrentios Kazantzidis - l.c.kazantzidis@gmail.com
Leandros Perivolaropoulos - leandros@uoi.gr
Foteini Skara - f.skara@uoi.gr
