w-M Phantom Transition at zt<0.1 as a Resolution of the Hubble Tension
Published in Physical Review D, 2020
Abstract
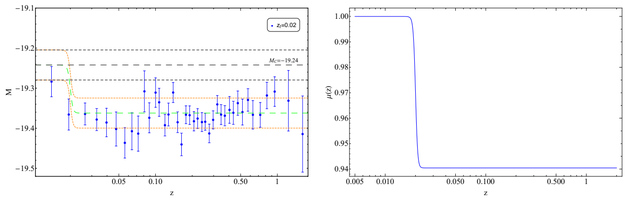
A rapid phantom transition of the dark energy equation of state parameter w at a transition redshift zt<0.1 of the form w(z)=-1+Δw·Θ(zt-z) with Δw<0 can lead to a higher value of the Hubble constant while closely mimicking a Planck18/ΛCDM form of the comoving distance for . Such a transition however would imply a significantly lower value of the SnIa absolute magnitude M than the value MC imposed by local Cepheid calibrators at z<0.01. Thus, in order to resolve the H0 tension it would need to be accompanied by a similar transition in the value of the SnIa absolute magnitude M as M(z)=MC+ΔM·Θ(z-zt) with ΔM<0. This is a Late w-M phantom transition (LwMPT). It may be achieved by a sudden reduction of the value of the normalized effective Newton constant μ=Geff/GN by about 6% assuming that the absolute luminosity of SnIa is proportional to the Chandrasekhar mass which varies as μ-3/2. We demonstrate that such an ultra low z abrupt feature of w-M provides a better fit to cosmological data compared to smooth late time deformations of H(z) that also address the Hubble tension. For zt=0.02 we find Δw≃-4, ΔM≃-0.1. This model also addresses the growth tension due to the predicted lower value of μ at z>zt. A prior of Δw=0 (no w transition) can still resolve the H0 tension with a larger amplitude M transition with ΔM≃-0.2 at zt≃0.01. This implies a larger reduction of μ for z>0.01 (about 12%). The LwMPT can be generically induced by a scalar field non-minimally coupled to gravity with no need of a screening mechanism since in this model μ=1 at z<0.01.
Cite
If you use any of the above codes or the figures in a published work please cite the following paper: w-M Phantom Transition at zt<0.1 as a Resolution of the Hubble Tension George Alestas, Lavrentios Kazantzidis and Leandros Perivolaropoulos Phys.Rev.D 103 (2021) 8, 083517, arxiv:2012.13932.
