H0 Tension, Phantom Dark Energy and Cosmological Parameter Degeneracies
Published in Physical Review D, 2020
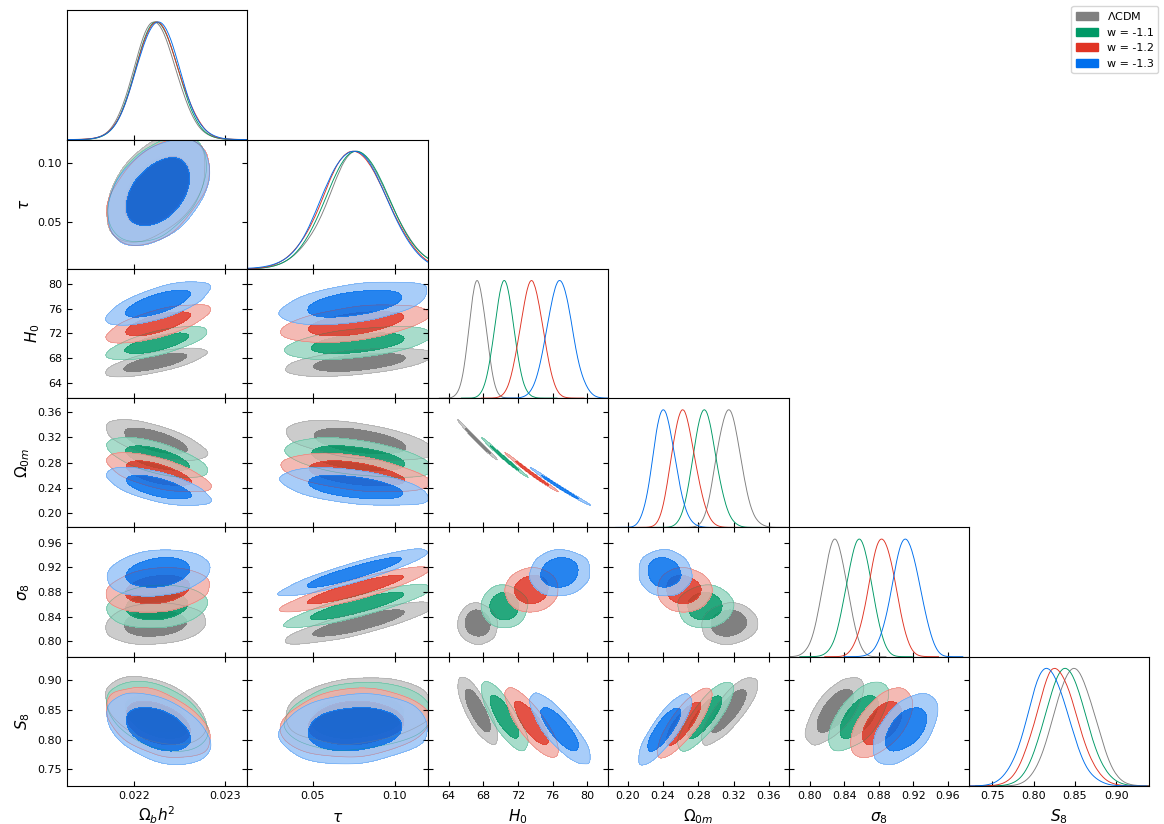
Abstract
Dark energy with equation of state parameter w<-1 can produce amplified cosmic acceleration at late times, thus increasing the value of H0 favoured by CMB data and releasing the tension with local measurements of H0. In order to demonstrate this hypothesis, we show that the best fit value of H0 in the context of the CMB power spectrum is degenerate with a constant equation of state parameter w, in accordance with the approximate effective linear equation H0+30.93·w-36.47=0 This equation is derived by assuming that both Ω0m·h2 and the co-moving angular diameter distance to the last scattering surface remain constant and equal to their best fit Planck/ΛCDM values as H0, Ω0m and w vary. This secures that the predicted CMB spectrum remains practically unchanged and equal to its best fit ΛCDM form. For w=-1, this linear degeneracy equation leads to the best fit H0=67.4 km sec-1 Mpc-1 as expected. For w=-1.22 the corresponding predicted CMB best fit Hubble constant is H0=74 km sec-1 Mpc-1 which is identical with the value obtained by local distance ladder measurements, therefore leading to an apparent resolution of the Hubble tension. We verify the above H0 degeneracy equation by fitting a wCDM model with fixed values of w to the Planck data and show that the above linear degeneracy equation is accurate to within less than 0.63% in the range -1.5<w<1, while the quality of fit to the Planck data remains practically unchanged in the parameter region. Finally we show how these results can be extended in the case of an evolving equation of state parameter w(z) leading to degenerate regions in the parameter space of parameters appearing in the form of w(z) where the predicted CMB power spectrum remains practically invariant. We analyse in detail this degeneracy for the CPL parametrization and identify analytically the full w0-w1 parameter region that leads to a best fit H0=74 km sec-1 Mpc-1 in the context of the Planck CMB spectrum.
Cite
If you use any of the above codes or the figures in a published work please cite the following paper: H0 Tension, Phantom Dark Energy and Cosmological Parameter Degeneracies George Alestas, Lavrentios Kazantzidis and Leandros Perivolaropoulos Phys.Rev.D 101 (2020) 12, 123516, arxiv:2004.08363.
